내용 정리

03-1 k-최근접 이웃 회귀

지도 학습 알고리즘은 크게 분류와 회귀로 나눠집니다.

내년도 경제 성장률을 예측하거나 배달이 도착할 시간을 예측하는 것이 회귀라고 볼 수 있습니다.

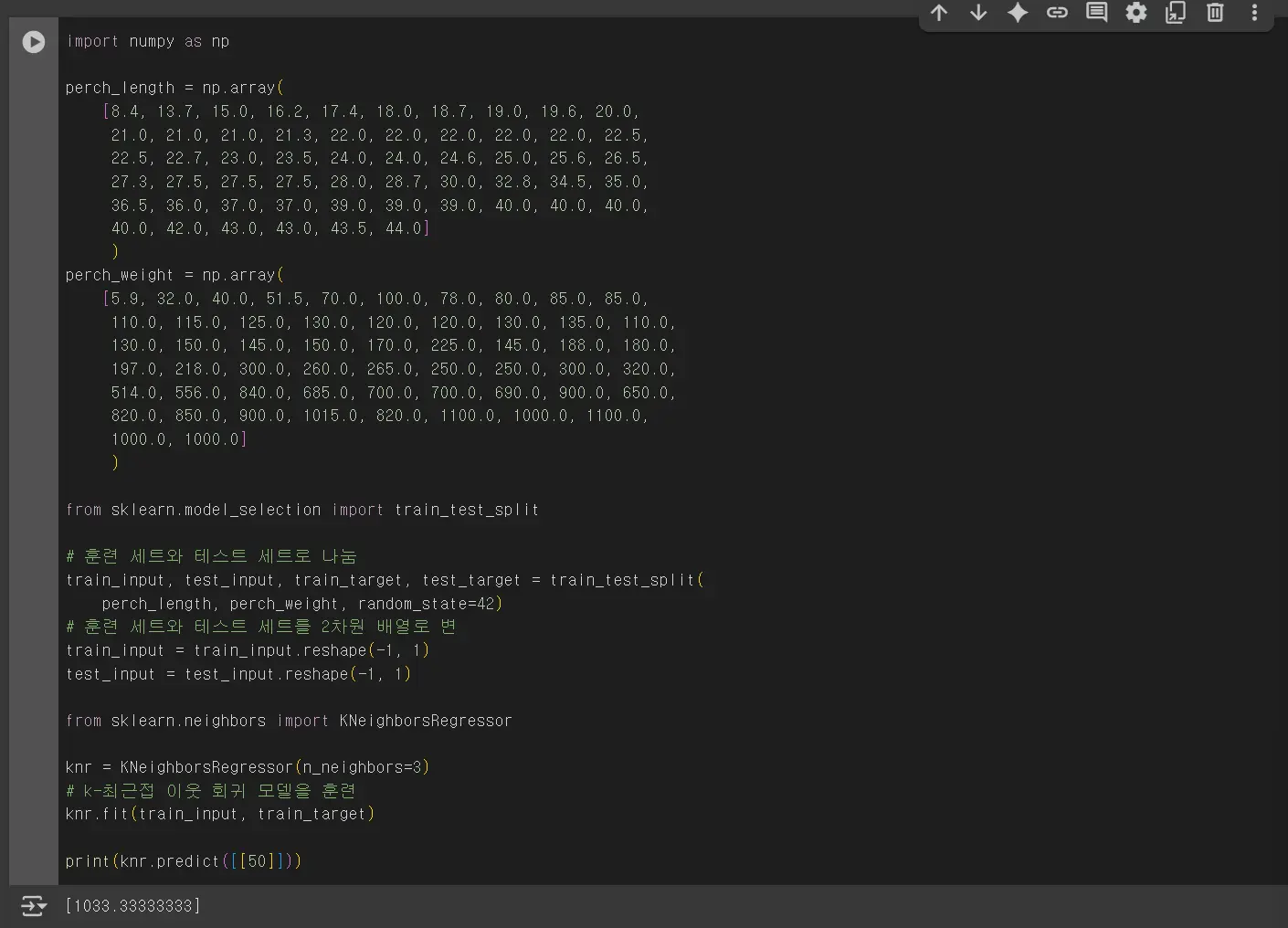
k-최근접 이웃 회귀는 분류와 똑같이 예측하려는 샘플에 가장 가까운 샘플 k개를 선택합니다. 해당 샘플의 평균을 구하면 됩니다.

데이터 준비

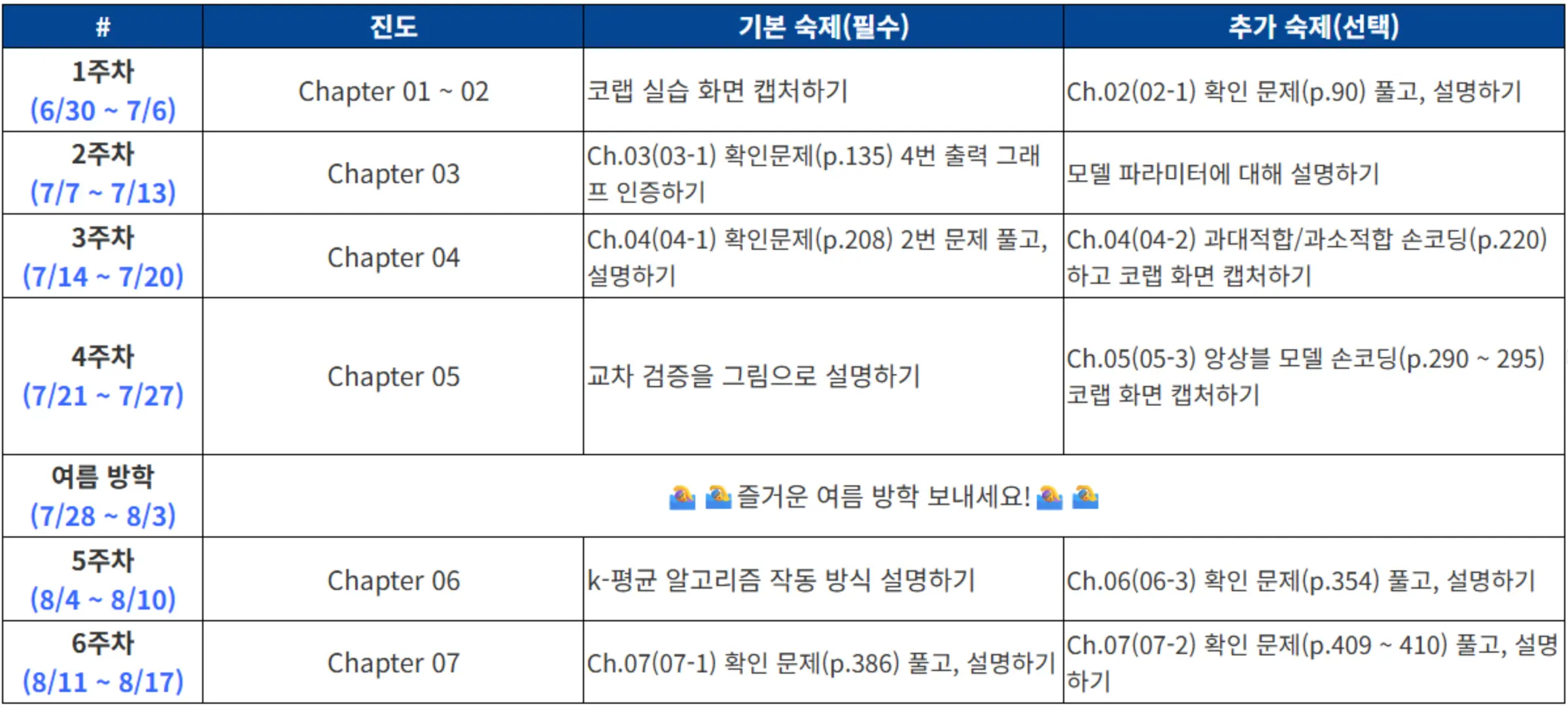
넘파이 배열로 샘플 데이터를 추가하고, 산점도 그리기

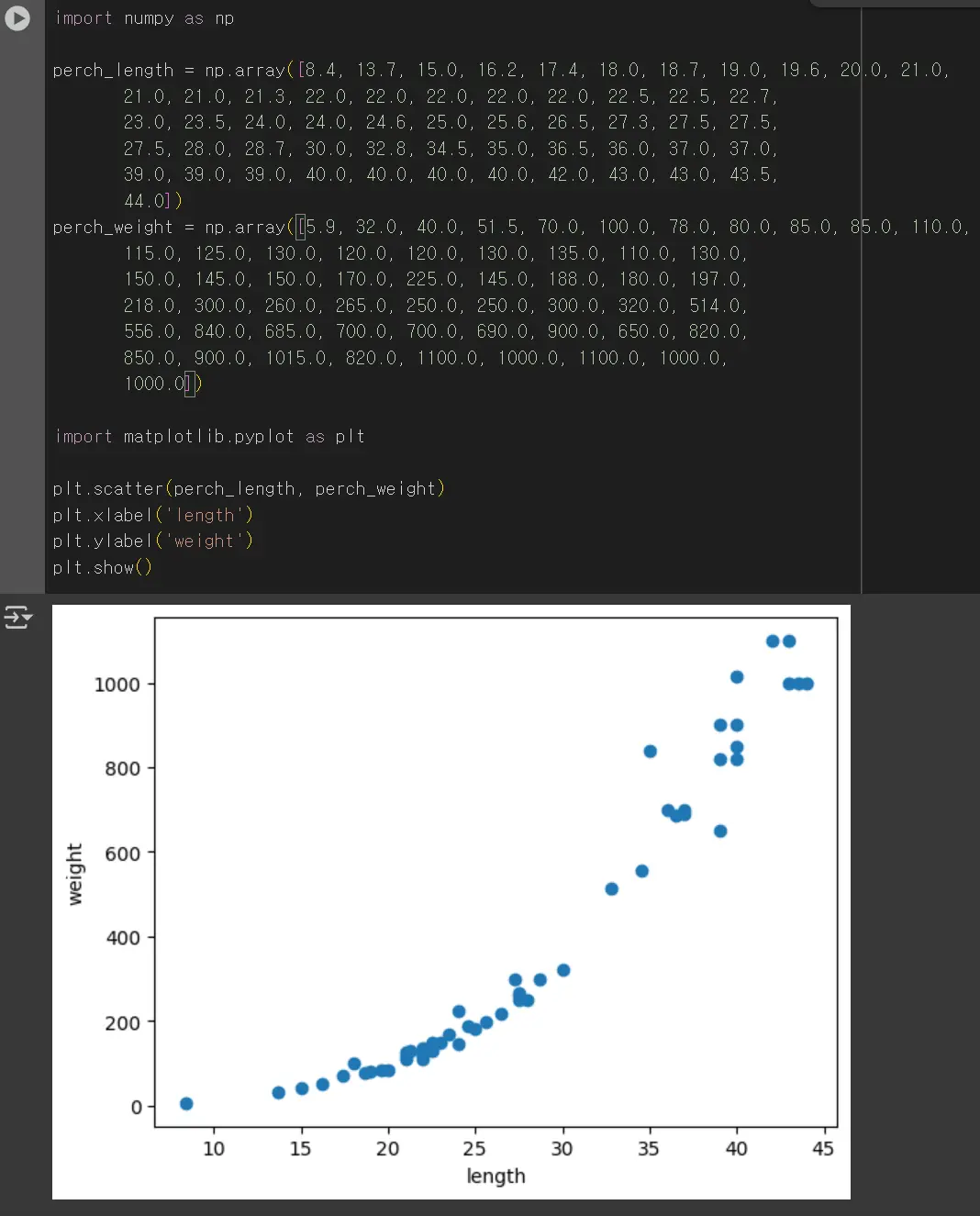
reshape() 메서드는 넘파이 배열의 크기를 바꿀 수 있는 함수입니다.

넘파이는 배열의 크기를 자동으로 지정하는 기능도 제공합니다. 크기에 -1을 지정하면 나머지 원소 개수로 모두 채우라는 의미입니다.

위의 (42, 1) (14, 1)은 훈련 데이터 42개 테스트 데이터 14개로 75:25 의 비율로 분류됩니다.

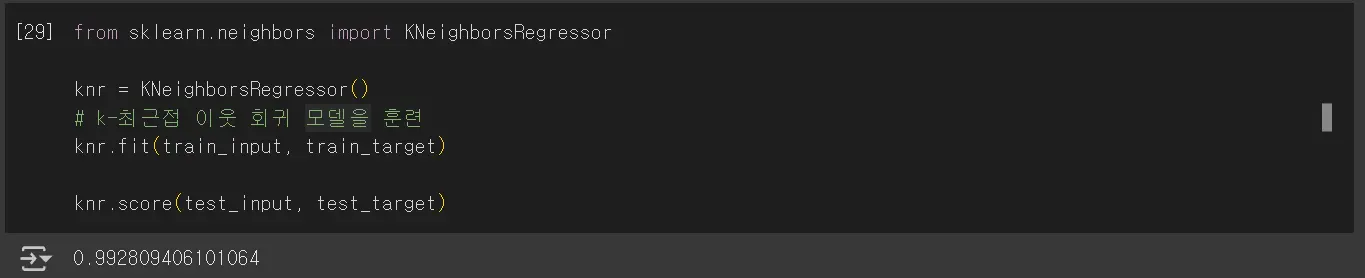
결정계수(R²)

회귀의 경우 결정계수를 이용하여 점수를 판단합니다. 1에 가까울수록 좋습니다.

mean_absolute_error는 타깃과 예측의 절댓값 오차를 평균하여 반환합니다.

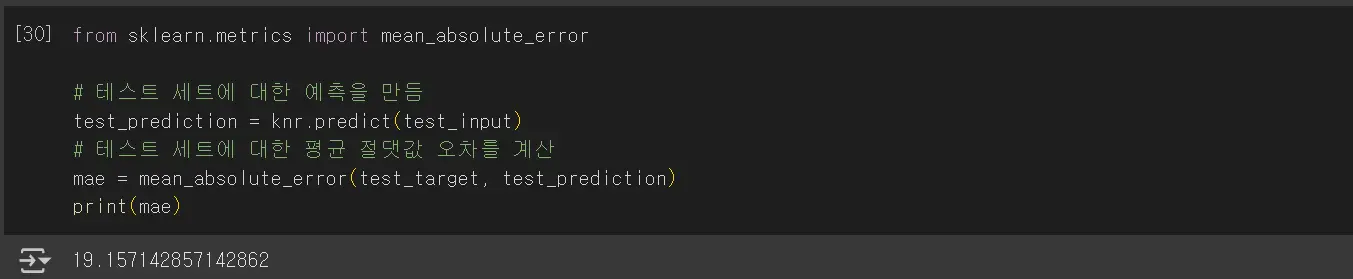
예측이 19g 정도의 무게값이 다르다는 예측을 함

과대적합 vs 과소적합

훈련 세트에서 점수가 굉장히 좋았는데 테스트 세트에서는 점수가 굉장히 나쁘다면 모델이 훈련 세트에 과대적합 되었다고 함

훈련 세트보다 테스트 세트의 점수가 높거나 두 점수가 모두 너무 낮은 경우는 훈련 세트에 과소적합 되었다고 함

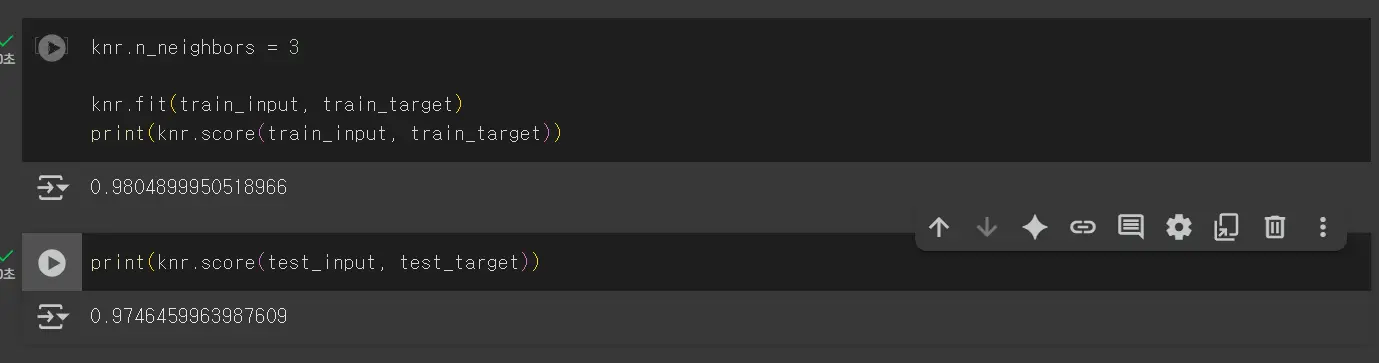
사이킷런의 k-최근접 이웃 알고리즘의 기본 k 값은 5이지만, 이 값을 바꾸면 점수에 영향을 줄 수 있습니다.

03-1 확인 문제

k-최근접 이웃 회귀 모델의 k 값을 1, 5, 10으로 바꿔서 진행합니다.

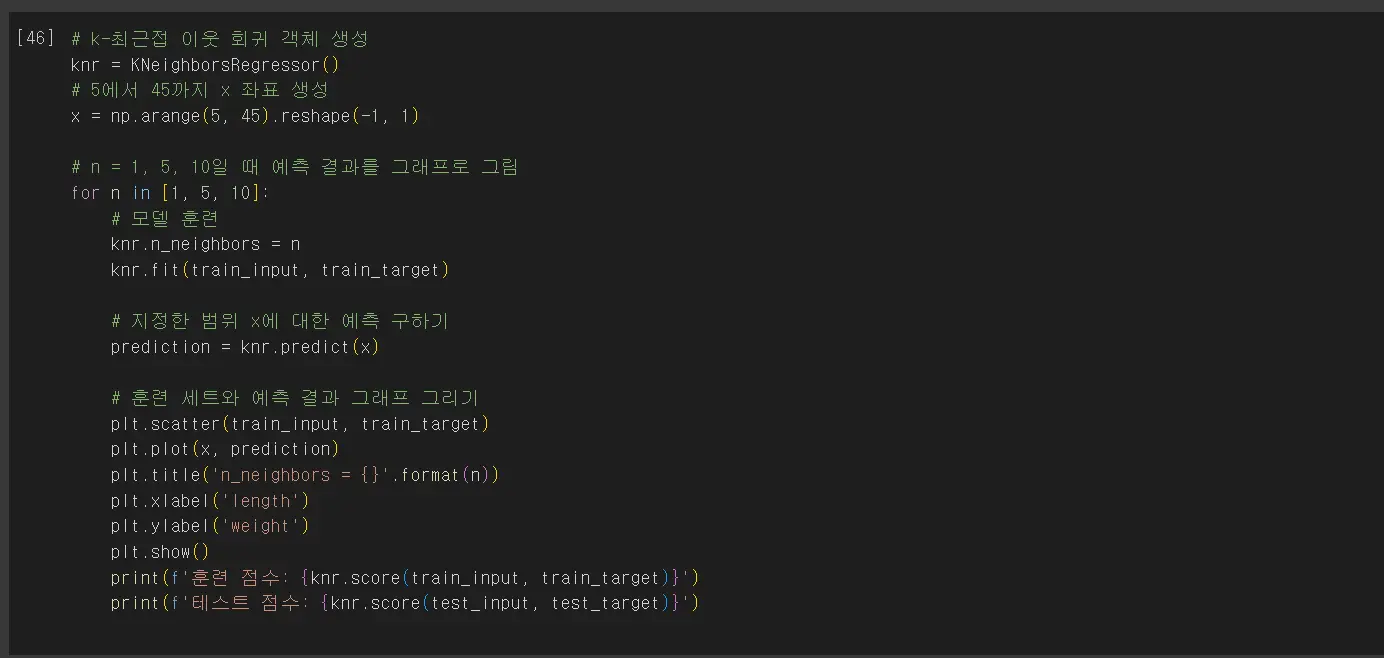
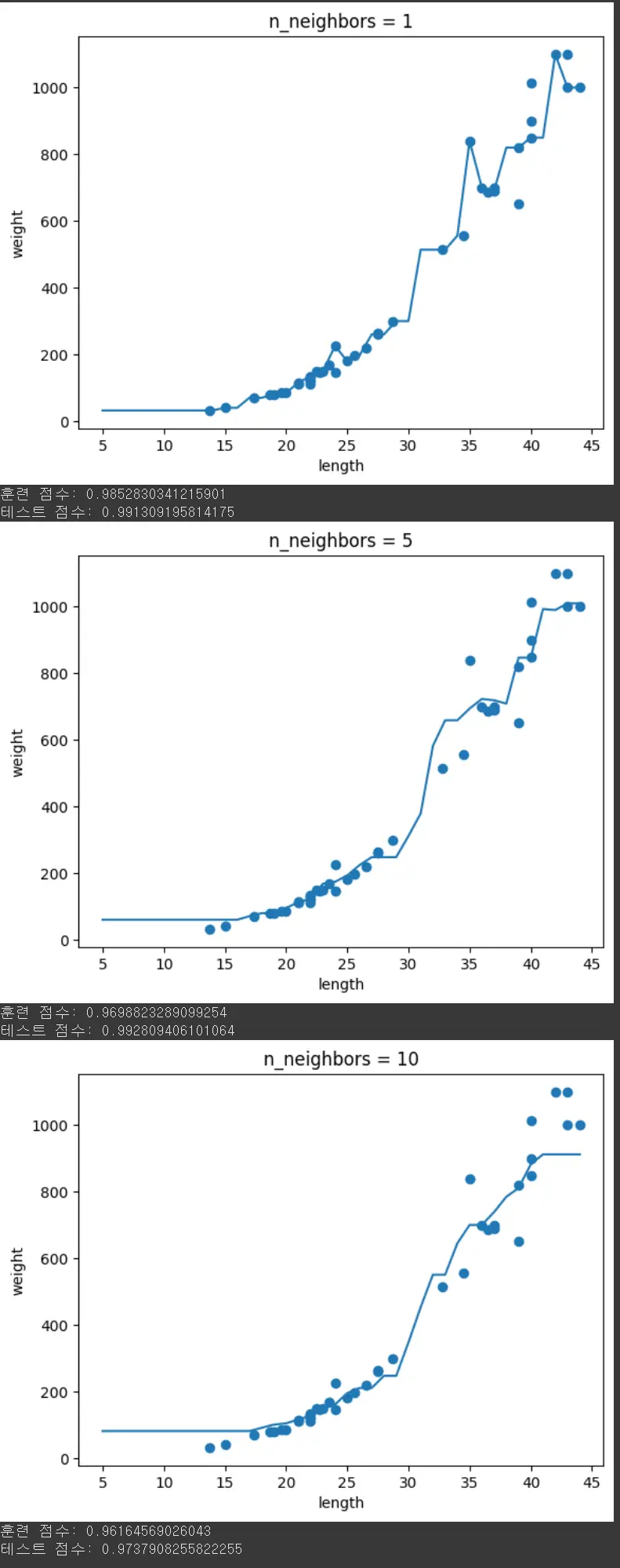
각 k값별 특징

k=1 (n_neighbors=1)

• 가장 가까운 1개 점만 사용해서 예측
• 예측선이 매우 구불구불하고 불규칙
• 훈련 데이터의 각 점에 민감하게 반응
• 과대적합 경향 - 노이즈까지 학습

k=5 (n_neighbors=5)

• 가장 가까운 5개 점의 평균으로 예측
• 예측선이 k=1보다 더 부드럽고 안정적
• 적절한 일반화 성능

k=10 (n_neighbors=10)

• 가장 가까운 10개 점의 평균으로 예측
• 예측선이 가장 부드럽고 단순
• 너무 단순해서 과소적합 가능성
• 점수도 3개 중에 제일 낮음

03-2 선형 회귀

선형 회귀는 널리 사용되는 대표적인 회귀 알고리즘입니다. 비교적 간단하고 성능이 뛰어나기 때문에 맨 처음 배우는 머신러닝 알고리즘 중 하나입니다.

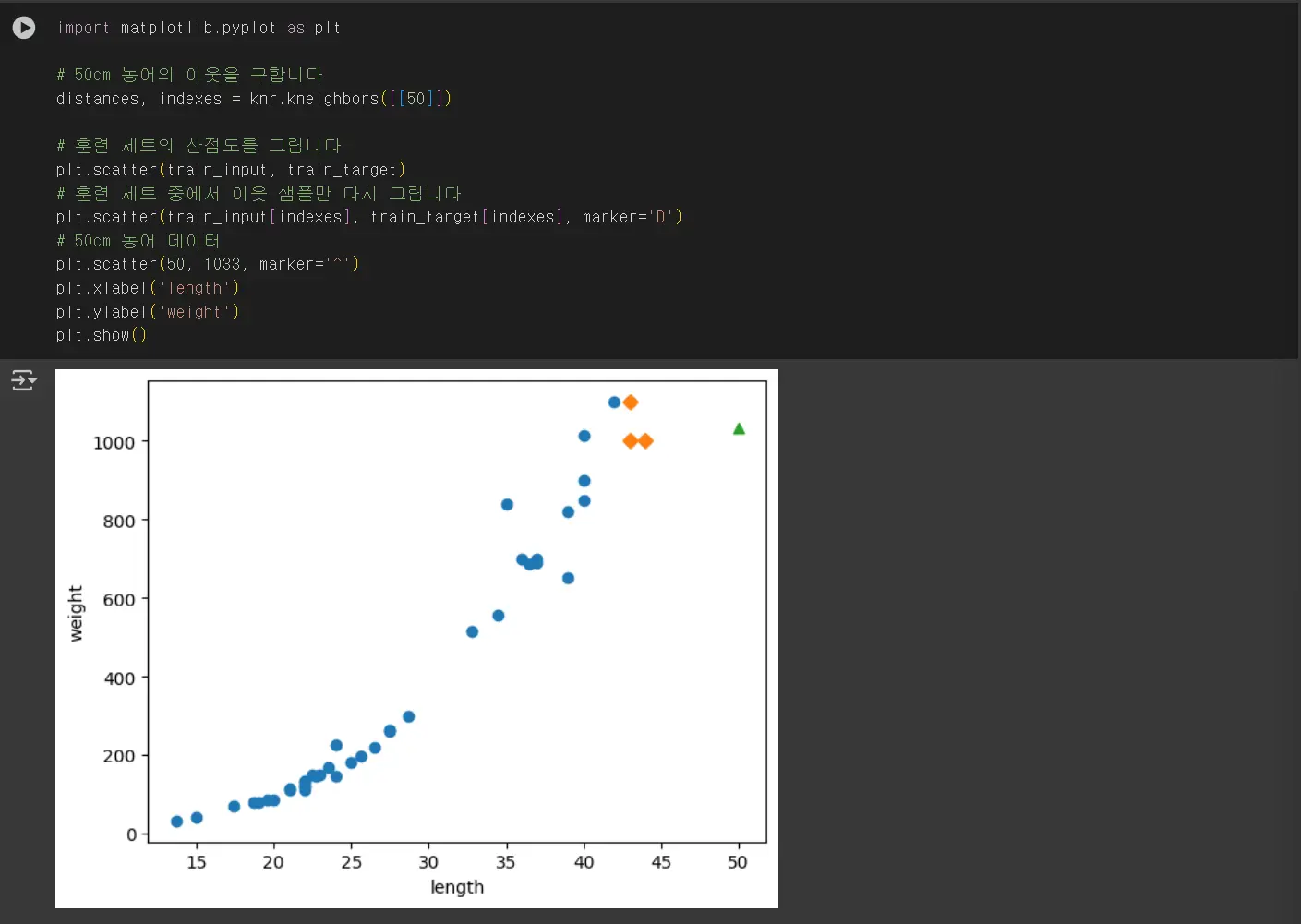
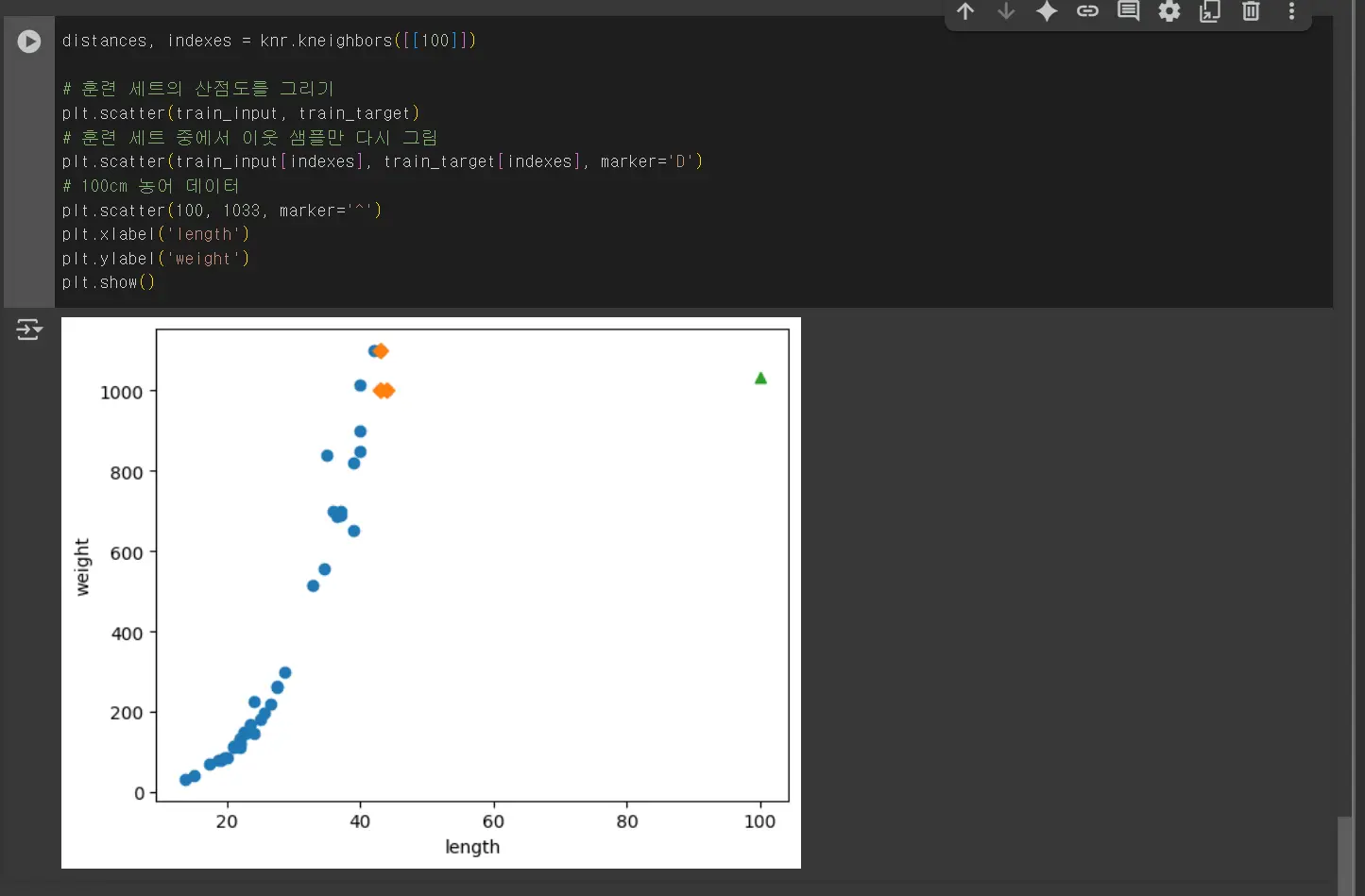
위와 같이 k-최근접 이웃을 사용해 이 문제를 해결하려면 가장 큰 농어가 포함되도록 훈련 세트를 다시 만들어야 합니다.

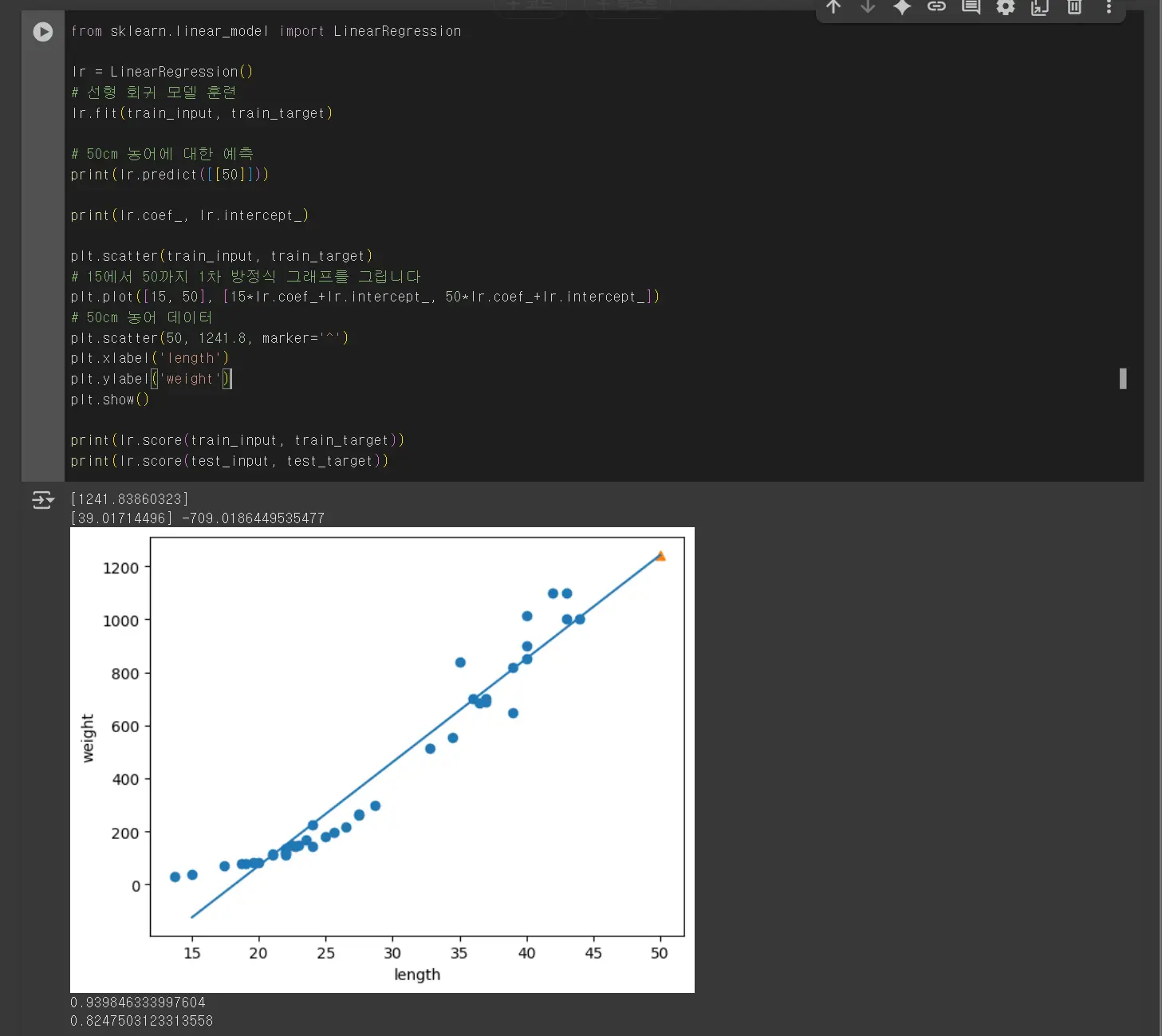
아래의 직선이 선형 회귀 알고리즘이 이 데이터셋에서 찾은 최적의 직선입니다.

다항 회귀

넘파이의 column_stack() 함수를 사용하여 데이터셋을 만듭니다.

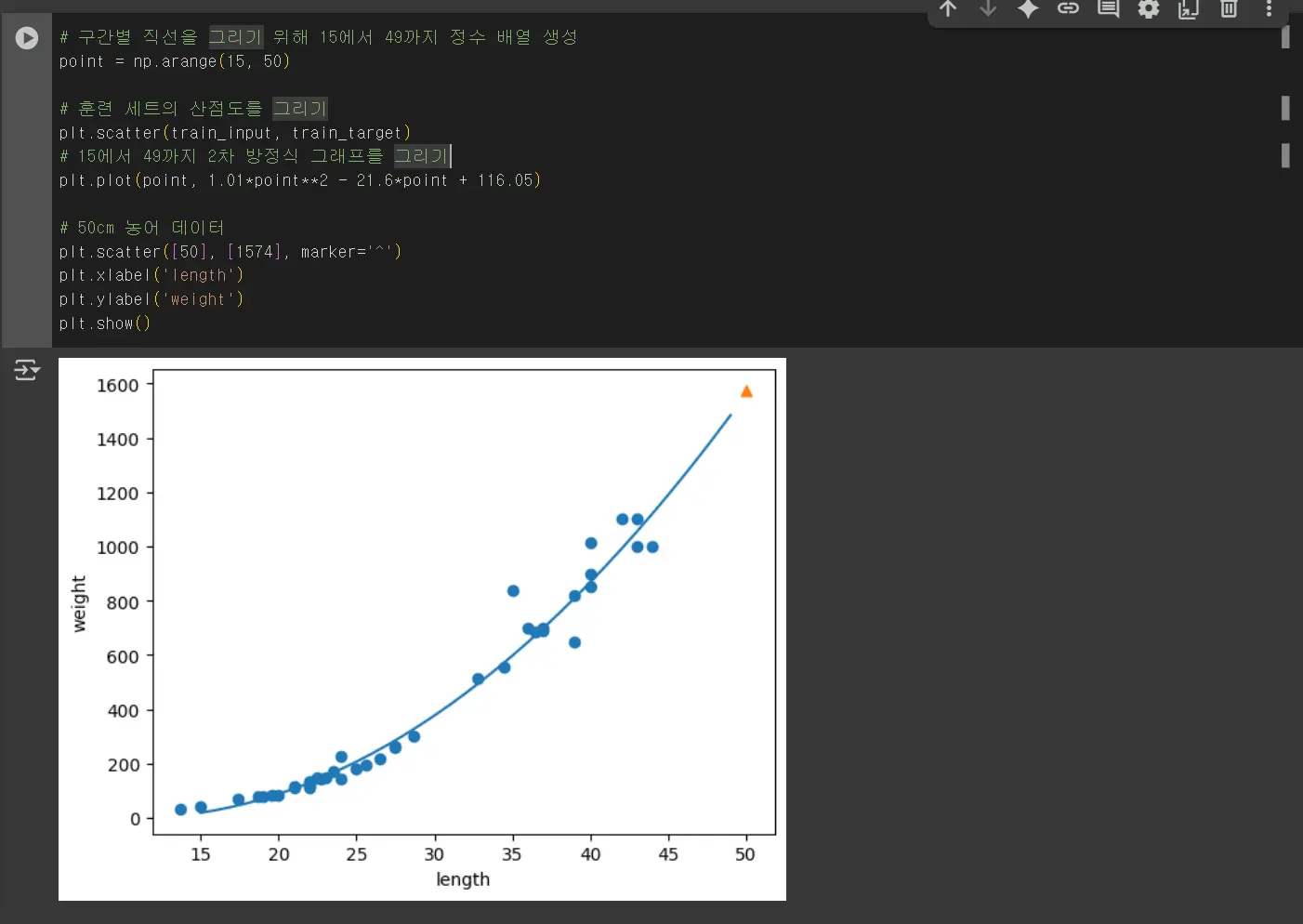
무게 = 1.01 x 길이제곱 - 21.6 * 길이 + 116.05

이런 방정식을 다항식이라 부르며 다항식을 사용한 선형 회귀를 다항 회귀라고 부릅니다.

k-최근접 이웃 회귀를 사용해서 농어의 무게를 예측할 때의 문제점은 훈련 세트 범위 밖의 샘플을 예측할 수 없다는 점입니다.

이를 해결하기 위해 선형 회귀를 사용합니다. 하지만 모델이 단순하여 농어의 무게가 음수일 수도 있습니다.

이를 해결하기 위해 다항 회귀를 사용합니다. 농어의 길이를 제곱하여 훈련 세트에 추가한 다음 선형 회귀 모델을 다시 훈련하는 방식입니다.

03-3 특성 공학의 규제

선형 회귀는 특성이 많을수록 엄청난 효과를 낸다고 합니다.

다중 회귀

여러 개의 특성을 사용한 선형 회귀를 다중 회귀라고 부릅니다.

판다스는 유명한 데이터 분석 라이브러리입니다. 데이터프레임은 판다스의 핵심 데이터 구조입니다.

사이킷런의 변환기

사이키럿은 특성을 만들거나 전처리하기 위한 다양한 클래스를 제공합니다. 사이킷런에서는 이런 클래스를 변환기라고 부릅니다.

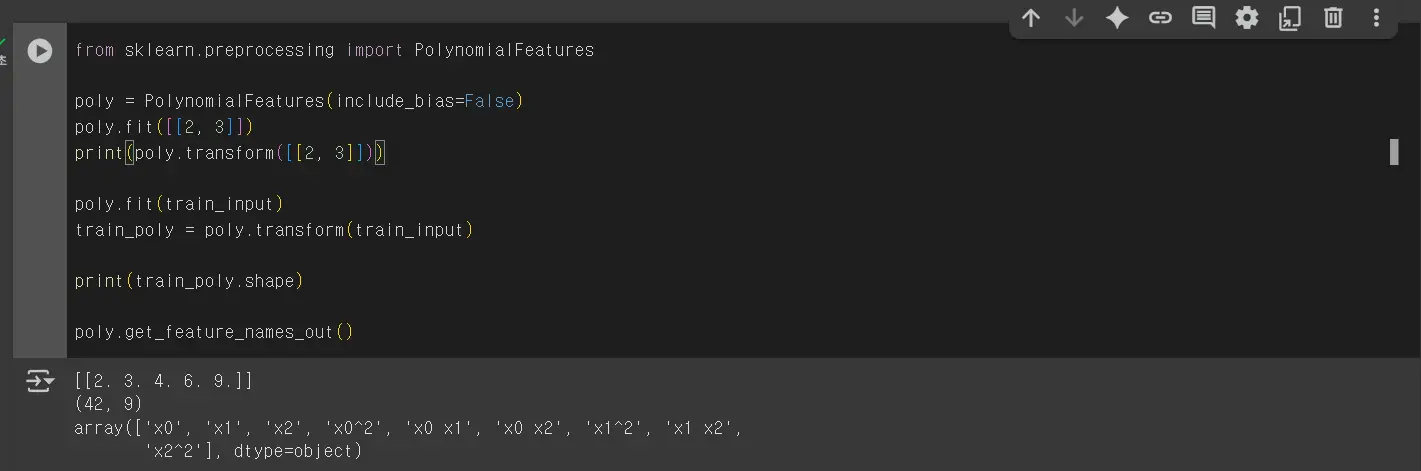
PolynomialFeatures 클래스는 9개의 특성이 어떻게 만들어졌는지 확인하는 함수를 제공합니다.

‘x0’은 첫 번째 특성을 의미하고 ‘x0^2’는 첫 번째 특성의 제곱, ‘x0 x1’은 첫 번째 특성과 두번째 특성의 곱을 나타내는 식입니다..

다중 회귀 모델 훈련하기

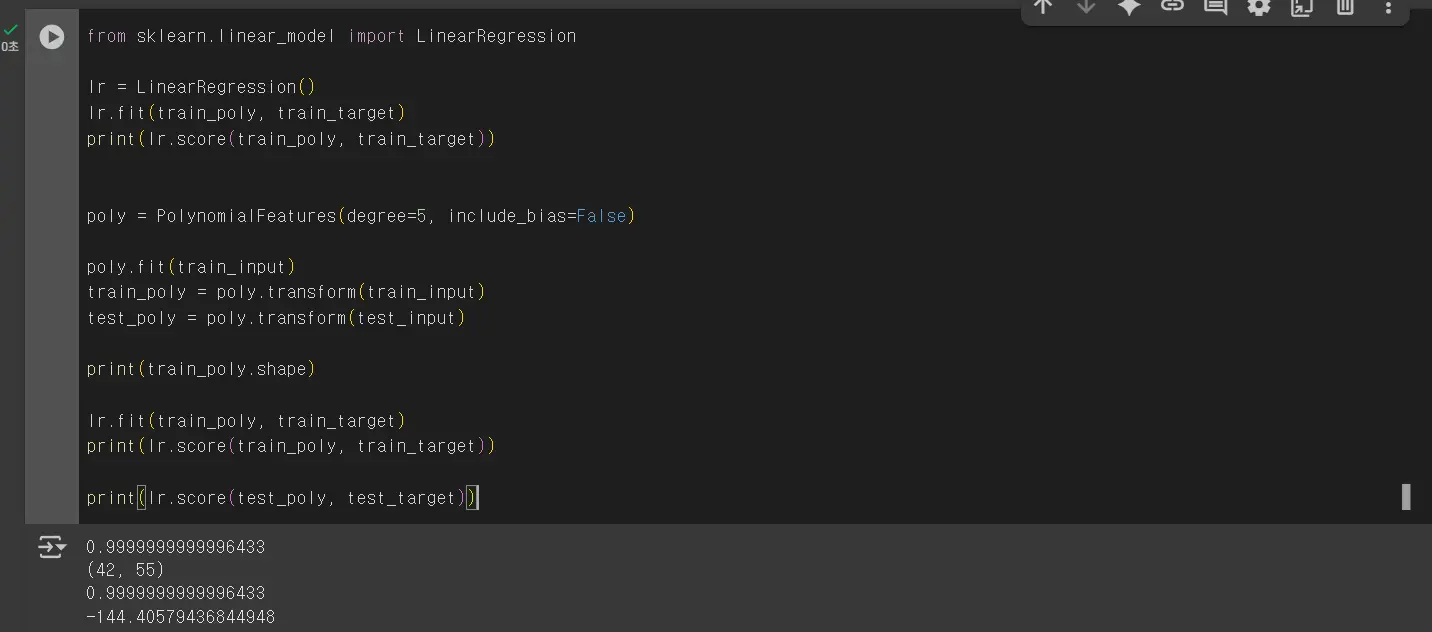
특성의 개수를 크게 늘리면 선형 모델은 아주 강력해집니다. 하지만 이런 모델은 훈련 세트에 너무 과대적합되므로 테스트 세트에서는 형편없는 점수를 만듭니다.

규제

규제는 머신러닝 모델이 훈련 세트를 너무 과도하게 학습하지 못하도록 훼방하는 것을 말합니다. 모델이 훈련 세트에 과대적합되지 않도록 만드는 것입니다.

선형 회귀 모델에 규제를 추가한 모델을 릿지와 라쏘라고 부릅니다.

릿지는 계수를 제곱한 값을 기준으로 규제를 적용하고, 라쏘는 계수의 절댓값을 기준으로 규제를 적용합니다.
일반적으로 릿지를 조금 더 선호한다고 합니다.

릿지 회귀

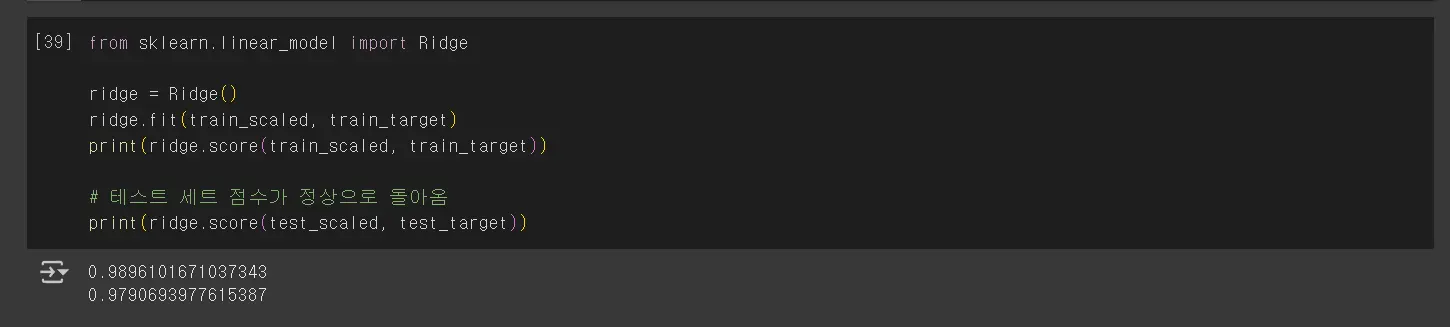
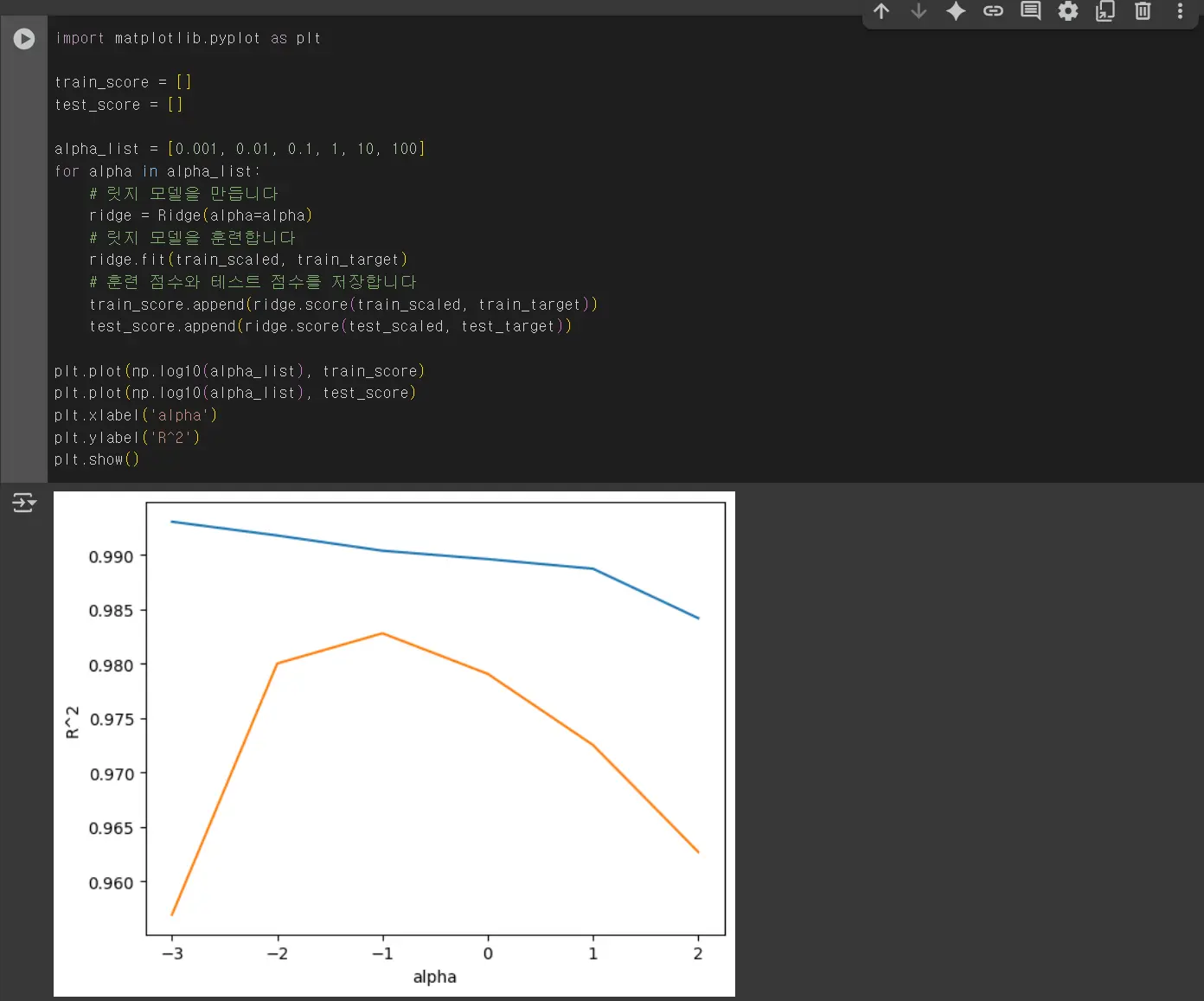
alpha 값을 0.001에서 100까지 10배씩 늘려가며 릿지 회귀 모델을 훈련한 다음 훈련 세트와 테스트 세트의 점수를 파이썬 리스트에 저장합니다.

라쏘 회귀

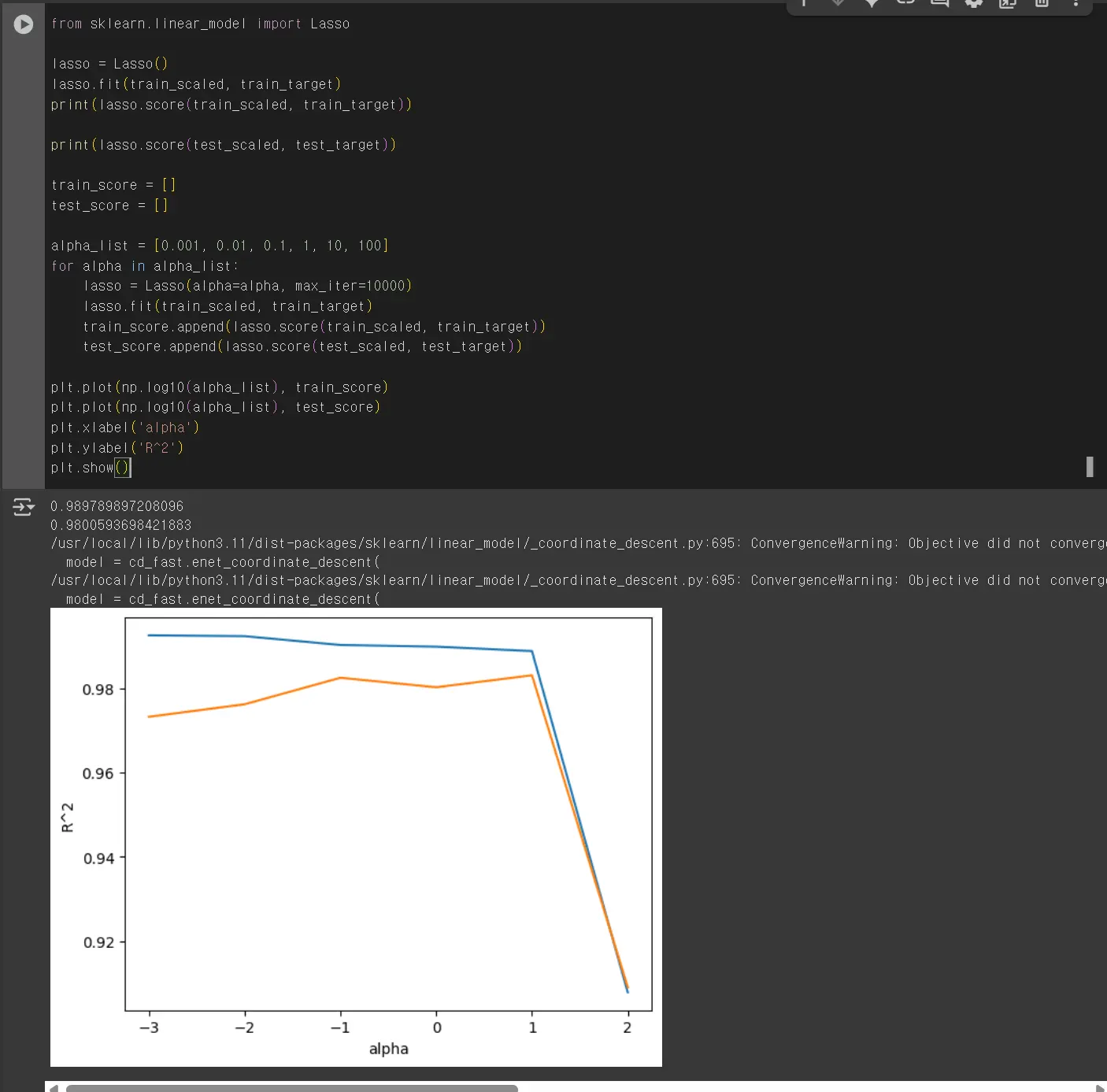
왼쪽은 과대적합을 보여주고 있고, 오른쪽으로 갈수록 훈련 세트와 테스트 세트의 점수가 좁혀지고 있습니다.

라쏘 모델은 계수 값을 0으로 만들 수 있습니다. 라쏘 모델의 계수를 coef_ 속성에 저장되어 있습니다.

55개의 특성 중 라쏘 모델이 사용한 특성은 15개 정도입니다.

이번 장에서는 다중 회귀, 특성 공학, 릿지, 라쏘 등에 알아볼 수 있었습니다.