[혼공머신] 6주차 학습 내용 정리

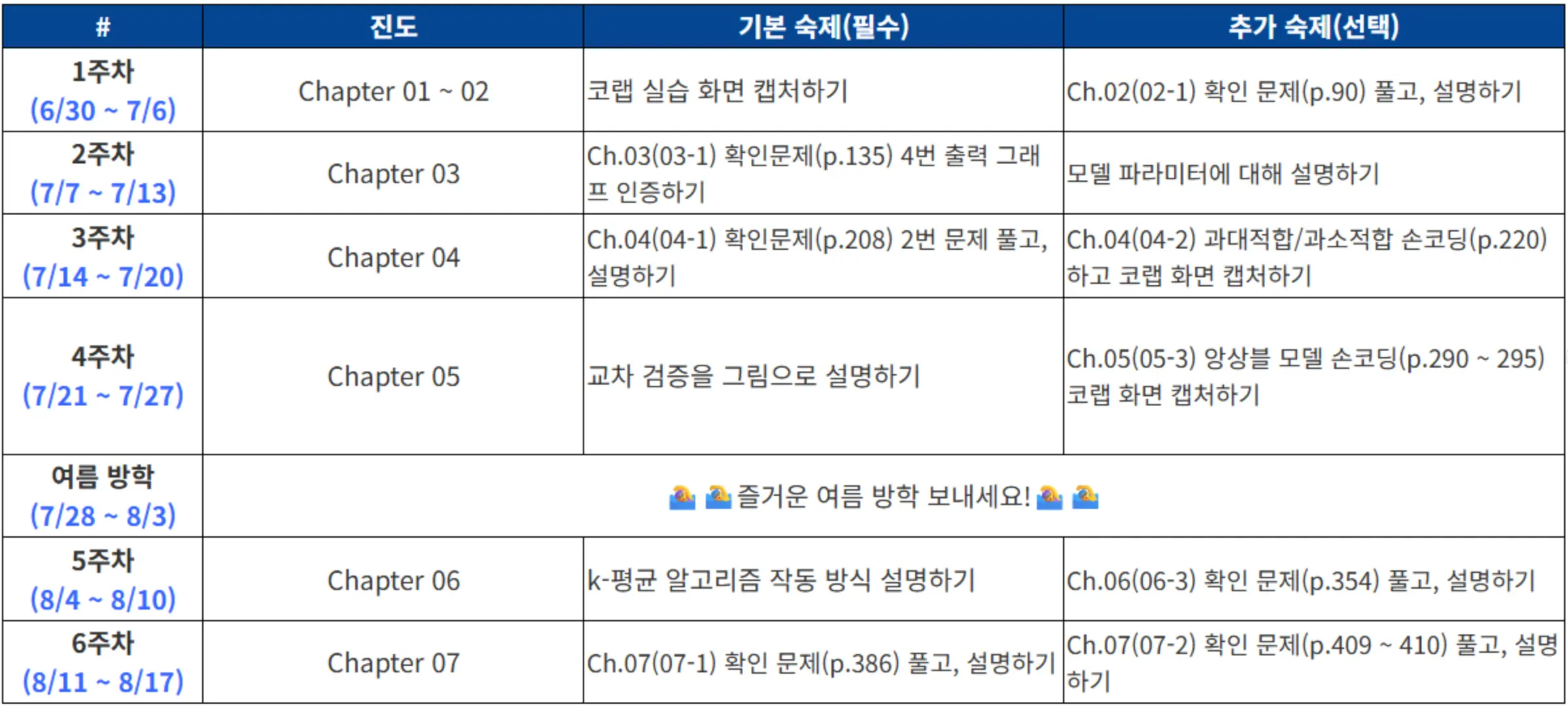
기본 숙제

인공 신경망의 입력 특성 100개, 밀집층 뉴런 개수 10개 일 때, 필요한 모델 파라미터 개수는 몇 개 인가요?

정답: 1,010개

파라미터 수 = (입력 특성 수 × 뉴런 수) + 뉴런 수 = (100 × 10) + 10 = 1,010개

케라스 Dense 클래스 사용해 신경망의 출력층을 만들려고 합니다. 이 신경망이 이진 분류 모델이라면 activation 매개변수에 어떤 활성화 함수를 지정해야 하나요?

정답 ‘sigmoid’

시그모이드는 출력을 0~1 사이의 확률값으로 변환해주기 때문에 이진 분류에 적합합니다.

케라스 모델에서 손실함수와 측정 지표 등을 지정하는 메서드는 무엇인가요?

정답: compile()

손실함수와 측정 지표를 지정하는 메서드입니다.

4. 정수 레이블을 타깃으로 가지는 다중 분류 문제일 때 케라스 모델의 compile() 메서드에 지정할 손실 함수로 적절한 것은 무언인가요?

정답: ‘sparse_categorical_crossentropy’

정수 형태의 레이블(예: 0, 1, 2, 3…)을 사용할 때는 sparse_categorical_crossentropy를, 원-핫 인코딩된 레이블을 사용할 때는 categorical_crossentropy를 사용합니다.

내용 정리

결국 딥러닝까지 오고 말았네요. 머신러닝도 잘 모르겠는데 딥러닝도 가볍게 찍먹할 수 있을지 모르겠네요.

딥러닝은 인공신경망(Neural Network)을 여러 층으로 깊게 쌓아서 복잡한 패턴을 학습하는 머신러닝의 한 분야라고 합니다.

딥러닝은 대량의 데이터와 연산력이 필요하지만, 기존 머신러닝으로는 해결하기 어려운 복잡한 문제들을 해결할 수 있는 강력한 도구입니다. 프레임워크로는 TensorFlow, PyTorch, Keras 등이 널리 사용됩니다.

패션 MINST 데이터를 텐서플로를 사용하여 데이터를 가져오는 실습을 합니다.

인공 신경망

텐서플로의 케라스 패키지를 임포트하여 패션 MINST 데이터를 다운로드 합니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 실행마다 동일한 결과를 얻기 위해 케라스에 랜덤 시드를 사용하고 텐서플로 연산을 결정적으로 만듭니다.
import tensorflow as tf

tf.keras.utils.set_random_seed(42)
tf.config.experimental.enable_op_determinism()

from tensorflow import keras

(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()

print(train_input.shape, train_target.shape) # 데이터 확인
print(test_input.shape, test_target.shape)

import matplotlib.pyplot as plt

fig, axs = plt.subplots(1, 10, figsize=(10,10))
for i in range(10):
    axs[i].imshow(train_input[i], cmap='gray_r')
    axs[i].axis('off')
plt.show()

# 샘플 타깃값(5는 신발로 유추)
print([train_target[i] for i in range(10)]) # [np.uint8(9), np.uint8(0), np.uint8(0), np.uint8(3), np.uint8(0), np.uint8(2), np.uint8(7), np.uint8(2), np.uint8(5), np.uint8(5)]

import numpy as np

print(np.unique(train_target, return_counts=True)) # (array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8), array([6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000]))

패션 MINST 데이터셋을 저장하고, 각 레이블마다 6,000개의 샘플이 들어 있는것을 확인했습니다.

로지스틱 회귀로 패션 아이템 분류하기

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
train_scaled = train_input / 255.0
train_scaled = train_scaled.reshape(-1, 28 * 28) # reshape 메서드를 이용하여 28 사이즈로 지정하면 첫 번째 차원(샘플 개수)은 변하지 않고 원본 데이터의 두 번째, 세 번째 차원이 1차원으로 합쳐짐

print(train_scaled.shape) # (60000, 784) 784개의 픽셀로 이루어진 60,000개의 샘플

from sklearn.model_selection import cross_validate
from sklearn.linear_model import SGDClassifier

sc = SGDClassifier(loss='log_loss', max_iter=5, random_state=42) # SGDClassifier 반복 횟수를 지정하여 점수 확인

scores = cross_validate(sc, train_scaled, train_target, n_jobs=-1)
print(np.mean(scores['test_score'])) # 0.8194166666666666

reshape 메서드를 이용하여 2차원 배열인 각 샘플을 1차원 배열로 바꿉니다.

SGDClassifier 클래스를 이용해 점수를 측정해봅니다. 값을 변경해도 점수가 유의미하게 변하지 않습니다.

아마 반복 횟수보다는 데이터 전처리나 하이퍼파라미터 튜닝이 더 효과적일 수 있습니다. 책에서도 이에 대해 10개의 방정식에 대한 모델 파라미터(가중치와 절편)을 찾는 방식으로 설명하고 있네요.

인공 신경망

인공신경망은 뇌의 뉴런을 모방해서 만든 기계학습 모델이에요. 여러 층의 노드들이 연결되어 있고, 데이터가 들어오면 각 연결에 있는 가중치를 곱해서 다음 층으로 전달하는 방식으로 작동합니다.

학습할 때는 예측 결과와 정답을 비교해서 오차를 계산하고, 이 오차를 뒤로 전파하면서 가중치들을 조금씩 수정해 나갑니다.

이 과정을 반복하면서 점점 더 정확한 예측을 할 수 있게됩니다다.

복잡한 패턴도 잘 찾아내지만 많은 데이터와 계산이 필요하고, 왜 그런 결과가 나왔는지 설명하기는 어려운 특징이 있습니다.

딥러닝 라이브러리가 다른 머신러닝 라이브러리와 다른 점 중 하나는 그래픽 처리 장치인 GPU를 사용하여 인공 신경망을 훈련하는 것입니다.

텐서플로에서 케라스를 사용하여 실습을 합니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
import tensorflow as tf

from tensorflow import keras

from sklearn.model_selection import train_test_split

train_scaled, val_scaled, train_target, val_target = train_test_split(
    train_scaled, train_target, test_size=0.2, random_state=42) # 테스트 사이즈 20프로

# 훈련 세트 48,000
print(train_scaled.shape, train_target.shape) # (48000, 784) (48000,)
# 검증 세트 12,000
print(val_scaled.shape, val_target.shape) # (12000, 784) (12000,)

# 케라스의 레이어 패키지안에 10개 뉴런 생성(이러한 연결을 완전 연결층이라고 부름)
dense = keras.layers.Dense(10, activation='softmax', input_shape=(784,)) # 뉴런 개수, 뉴런의 출력에 적용할 함수, 입력의 크기

model = keras.Sequential([dense]) # 계산 결과에 적용되는 함수를 활성화 함수 라고 부름

인공 신경망으로 패션 아이템 분류하기

케라스에서 사용하는 함수에 대해 설명해주네요.

신경망은 티셔츠 샘플에서 손실을 낮추려면 첫 번째 뉴런의 활성화 출력의 값을 가능한 1에 가깝게 만들어야 합니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
model.compile(loss='sparse_categorical_crossentropy', metrics=['accuracy'])

model.fit(train_scaled, train_target, epochs=5) # 모델 훈련

Epoch 1/5
1200/1200 ━━━━━━━━━━━━━━━━━━━━ 5s 3ms/step - accuracy: 0.7194 - loss: 0.8260
Epoch 2/5
1200/1200 ━━━━━━━━━━━━━━━━━━━━ 4s 2ms/step - accuracy: 0.8308 - loss: 0.4937
Epoch 3/5
1200/1200 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - accuracy: 0.8417 - loss: 0.4607
Epoch 4/5
1200/1200 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - accuracy: 0.8467 - loss: 0.4443
Epoch 5/5
1200/1200 ━━━━━━━━━━━━━━━━━━━━ 3s 3ms/step - accuracy: 0.8505 - loss: 0.4339

model.evaluate(val_scaled, val_target) # 모델 평가

300/300 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - accuracy: 0.8647 - loss: 0.4184
[0.4308134913444519, 0.8594791889190674]

심층 신경망

심층 신경망은 은닉층이 2개 이상인 깊은 구조의 신경망을 말합니다. 일반적인 신경망보다 훨씬 많은 층을 쌓아서 더 복잡하고 추상적인 패턴을 학습할 수 있습니다.

층이 깊어질수록 저수준 특성(예: 선, 모서리)부터 고수준 특성(예: 눈, 코, 얼굴)까지 단계적으로 학습하게 되죠. 이미지 인식에서는 첫 번째 층에서 간단한 선을 감지하다가 마지막 층에서는 완전한 객체를 인식할 수 있게 됩니다.

하지만 층이 깊어지면 그래디언트 소실 문제나 과적합 같은 문제가 생기기 쉬워서, 이를 해결하기 위해 렐루루 함수나 드롭아웃, 배치 정규화 같은 기법들을 사용합니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
from tensorflow import keras

(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()

from sklearn.model_selection import train_test_split

train_scaled = train_input / 255.0
train_scaled = train_scaled.reshape(-1, 28*28)

train_scaled, val_scaled, train_target, val_target = train_test_split(
    train_scaled, train_target, test_size=0.2, random_state=42)


dense1 = keras.layers.Dense(100, activation='sigmoid', input_shape=(784,))
dense2 = keras.layers.Dense(10, activation='softmax')
# 심층 신경망 만들기
model = keras.Sequential([dense1, dense2])
# 케라스에서 모델 summary 호출 시 여러 유용한 정보를 볼 수 있음
model.summary()
# ---
# Model: "sequential_2"
# ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
# ┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
# ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
# │ dense_2 (Dense)                 │ (None, 100)            │        78,500 │
# ├─────────────────────────────────┼────────────────────────┼───────────────┤
# │ dense_3 (Dense)                 │ (None, 10)             │         1,010 │
# └─────────────────────────────────┴────────────────────────┴───────────────┘
#  Total params: 79,510 (310.59 KB)
#  Trainable params: 79,510 (310.59 KB)
#  Non-trainable params: 0 (0.00 B)
# ---

model = keras.Sequential([
    keras.layers.Dense(100, activation='sigmoid', input_shape=(784,), name='hidden'),
    keras.layers.Dense(10, activation='softmax', name='output')
], name='패션 MNIST 모델')

model.summary()
# ---
# Model: "패션 MNIST 모델"
# ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
# ┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
# ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
# │ hidden (Dense)                  │ (None, 100)            │        78,500 │
# ├─────────────────────────────────┼────────────────────────┼───────────────┤
# │ output (Dense)                  │ (None, 10)             │         1,010 │
# └─────────────────────────────────┴────────────────────────┴───────────────┘
#  Total params: 79,510 (310.59 KB)
#  Trainable params: 79,510 (310.59 KB)
#  Non-trainable params: 0 (0.00 B)
# ---

model.compile(loss='sparse_categorical_crossentropy', metrics=['accuracy'])

model.fit(train_scaled, train_target, epochs=5)
# ---
# Epoch 1/5
# 1500/1500 ━━━━━━━━━━━━━━━━━━━━ 9s 5ms/step - accuracy: 0.7480 - loss: 0.7737
# Epoch 2/5
# 1500/1500 ━━━━━━━━━━━━━━━━━━━━ 8s 3ms/step - accuracy: 0.8461 - loss: 0.4244
# Epoch 3/5
# 1500/1500 ━━━━━━━━━━━━━━━━━━━━ 6s 4ms/step - accuracy: 0.8601 - loss: 0.3836
# Epoch 4/5
# 1500/1500 ━━━━━━━━━━━━━━━━━━━━ 10s 3ms/step - accuracy: 0.8691 - loss: 0.3583
# Epoch 5/5
# 1500/1500 ━━━━━━━━━━━━━━━━━━━━ 5s 3ms/step - accuracy: 0.8764 - loss: 0.3394
# <keras.src.callbacks.history.History at 0x7944fd5f4dd0>
# ---

인공 신경망에 몇 개의 층을 추가하더라도 compile() 메서드와 fit() 메서드의 사용법은 동일합니다.

1절보다 조금 더 정확도가 올라가긴 했네요.

렐루 함수

ReLU는 “Rectified Linear Unit"의 줄임말로, 입력값이 양수면 그대로 출력하고 음수면 0으로 만드는 아주 간단한 함수입니다. 수식으로는 max(0, x)죠.

기존 시그모이드 함수보다 계산이 빠르고, 그래디언트 소실 문제도 덜해서 심층 신경망에서 많이 사용됩니다.

옵티마이저는 신경망의 가중치를 어떻게 업데이트할지 결정하는 알고리즘이에요. 기본적인 경사하강법부터 시작해서 Adam, RMSprop 같은 고급 버전들이 있습니다.

Adam은 현재 가장 널리 쓰이는 옵티마이저로, 각 파라미터마다 학습률을 적응적으로 조절해서 빠르고 안정적인 학습이 가능합니다.

대부분의 경우에서 좋은 성능을 보여줘서 기본 선택지로 많이 사용됩니다.

아래는 렐루 함수 정도만 실습한 내용입니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
model = keras.Sequential()
model.add(keras.layers.Flatten(input_shape=(28, 28)))
model.add(keras.layers.Dense(100, activation='relu')) # 렐루 사용
model.add(keras.layers.Dense(10, activation='softmax'))

model.summary()
# ---
# Model: "sequential_8"
# ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
# ┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
# ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
# │ flatten (Flatten)               │ (None, 784)            │             0 │
# ├─────────────────────────────────┼────────────────────────┼───────────────┤
# │ dense_14 (Dense)                │ (None, 100)            │        78,500 │
# ├─────────────────────────────────┼────────────────────────┼───────────────┤
# │ dense_15 (Dense)                │ (None, 10)             │         1,010 │
# └─────────────────────────────────┴────────────────────────┴───────────────┘
#  Total params: 79,510 (310.59 KB)
#  Trainable params: 79,510 (310.59 KB)
#  Non-trainable params: 0 (0.00 B)
# ---
(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()

train_scaled = train_input / 255.0

train_scaled, val_scaled, train_target, val_target = train_test_split(
    train_scaled, train_target, test_size=0.2, random_state=42)

model.compile(loss='sparse_categorical_crossentropy', metrics=['accuracy'])

model.fit(train_scaled, train_target, epochs=5)

model.evaluate(val_scaled, val_target)
# ---
# Epoch 1/5
# 1500/1500 ━━━━━━━━━━━━━━━━━━━━ 5s 3ms/step - accuracy: 0.7634 - loss: 0.6731
# Epoch 2/5
# 1500/1500 ━━━━━━━━━━━━━━━━━━━━ 5s 4ms/step - accuracy: 0.8523 - loss: 0.4072
# Epoch 3/5
# 1500/1500 ━━━━━━━━━━━━━━━━━━━━ 4s 3ms/step - accuracy: 0.8688 - loss: 0.3604
# Epoch 4/5
# 1500/1500 ━━━━━━━━━━━━━━━━━━━━ 5s 3ms/step - accuracy: 0.8801 - loss: 0.3345
# Epoch 5/5
# 1500/1500 ━━━━━━━━━━━━━━━━━━━━ 6s 4ms/step - accuracy: 0.8858 - loss: 0.3163
# 375/375 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - accuracy: 0.8762 - loss: 0.3714
# [0.37396520376205444, 0.872083306312561]
# ---

신경망 모델 훈련

케라스 API를 활용해 예제를 실습합니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
from tensorflow import keras
from sklearn.model_selection import train_test_split

(train_input, train_target), (test_input, test_target) = \
    keras.datasets.fashion_mnist.load_data()

train_scaled = train_input / 255.0

train_scaled, val_scaled, train_target, val_target = train_test_split(
    train_scaled, train_target, test_size=0.2, random_state=42)

# 모델 함수 생성
def model_fn(a_layer=None):
    model = keras.Sequential()
    model.add(keras.layers.Flatten(input_shape=(28, 28)))
    model.add(keras.layers.Dense(100, activation='relu'))
    if a_layer:
        model.add(a_layer)
    model.add(keras.layers.Dense(10, activation='softmax'))
    return model

model = model_fn()
model.summary()

model.compile(loss='sparse_categorical_crossentropy', metrics=['accuracy'])

history = model.fit(train_scaled, train_target, epochs=5, verbose=0) # verbose 훈련 과정 출력을 조정 0으로 지정하면 훈련 과정 나타내지 않음
print(history.history.keys()) # dict_keys(['accuracy', 'loss'])

import matplotlib.pyplot as plt

plt.plot(history.history['loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()

# 정확도 출력
plt.plot(history.history['accuracy'])
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()


model = model_fn()
model.compile(loss='sparse_categorical_crossentropy', metrics=['accuracy'])
# 에포크를 20으로 변경하여 테스트
history = model.fit(train_scaled, train_target, epochs=20, verbose=0)
plt.plot(history.history['loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()

검증 손실

손실을 사용하여 과대/과소 적합을 알 수 있는 방법에 대해 공부합니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
model = model_fn()
model.compile(loss='sparse_categorical_crossentropy', metrics=['accuracy'])

# 케라스 모델의 fit에 검증 데이터를 전달
history = model.fit(train_scaled, train_target, epochs=20, verbose=0,
                    validation_data=(val_scaled, val_target))

print(history.history.keys()) # dict_keys(['accuracy', 'loss', 'val_accuracy', 'val_loss'])

plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['train', 'val'])
plt.show()

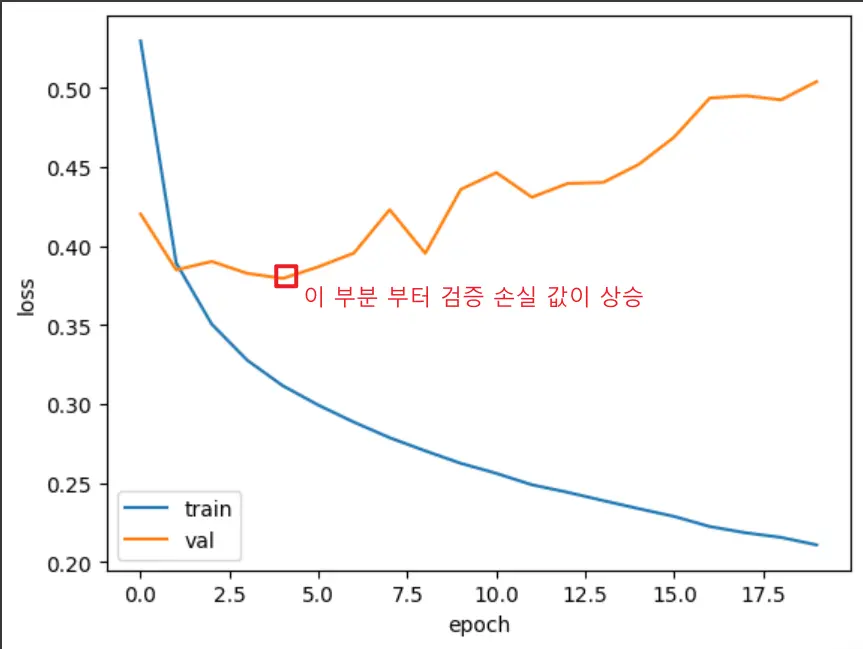
훈련 손실은 꾸준히 감소하기 때문에 전형적인 과대적합 모델이 만들어집니다. 검증 손실이 상승하는 시점을 가능한 뒤로 늦추면 검증 세트에 대한 손실이 줄어들 뿐만 아니라 검증 세트에 대한 정확도도 증가할 것 입니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
model = model_fn()
# Adam 옵티마이저를 적용
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

history = model.fit(train_scaled, train_target, epochs=20, verbose=0,
                    validation_data=(val_scaled, val_target))

plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['train', 'val'])
plt.show()

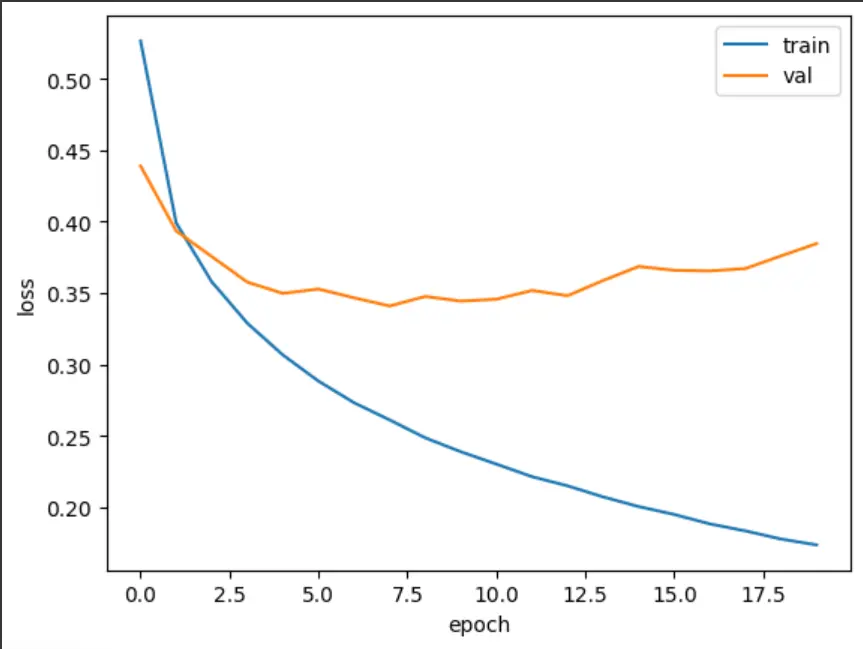
Adam 옵티마이저를 활용하니 검증 손실에 대한 수치가 조금 더 안정적으로 나왔습니다.

드롭 아웃

드롭아웃은 훈련 중에 일정 비율의 뉴런을 랜덤하게 “끄는” 정규화 기법입니다.

이렇게 하면 네트워크가 특정 뉴런에만 의존하지 않고 여러 뉴런을 골고루 사용하게 되어서 과적합을 방지할 수 있습니다.

마치 팀에서 특정 멤버에게만 의존하지 않고 모든 멤버가 역할을 할 수 있게 훈련하는 것과 비슷하죠.

중요한 점은 훈련할 때만 드롭아웃을 적용하고, 실제 예측할 때는 모든 뉴런을 사용합니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
model = model_fn(keras.layers.Dropout(0.3))

model.summary()
# ---
# Model: "sequential_13"
# ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
# ┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
# ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
# │ flatten_5 (Flatten)             │ (None, 784)            │             0 │
# ├─────────────────────────────────┼────────────────────────┼───────────────┤
# │ dense_24 (Dense)                │ (None, 100)            │        78,500 │
# ├─────────────────────────────────┼────────────────────────┼───────────────┤
# │ dropout (Dropout)               │ (None, 100)            │             0 │
# ├─────────────────────────────────┼────────────────────────┼───────────────┤
# │ dense_25 (Dense)                │ (None, 10)             │         1,010 │
# └─────────────────────────────────┴────────────────────────┴───────────────┘
#  Total params: 79,510 (310.59 KB)
#  Trainable params: 79,510 (310.59 KB)
#  Non-trainable params: 0 (0.00 B)
# ---
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

history = model.fit(train_scaled, train_target, epochs=20, verbose=0,
                    validation_data=(val_scaled, val_target))

plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['train', 'val'])
plt.show()

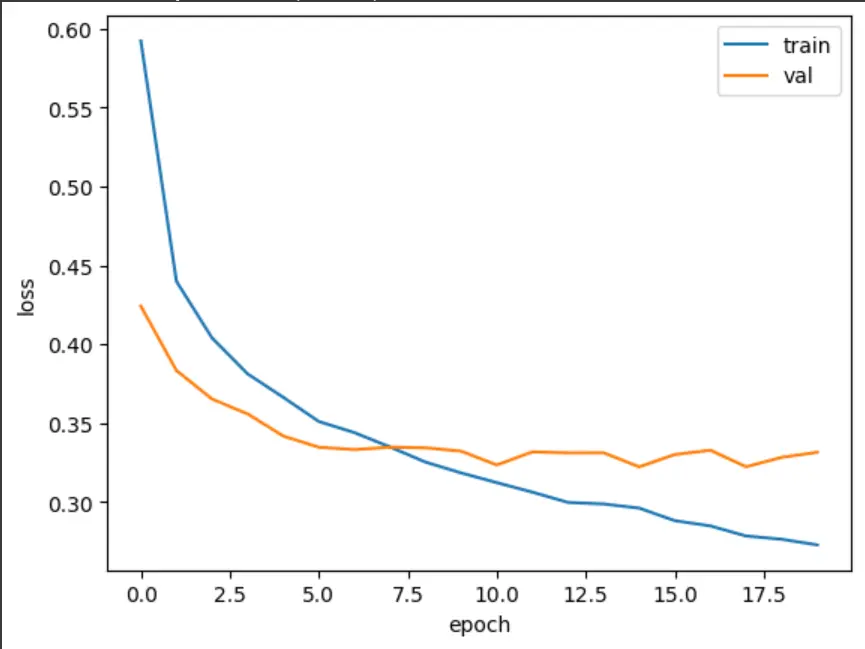
과대 적합이 확실히 줄어든 그래프를 확인할 수 있습니다.

모델 저장과 복원

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
model = model_fn(keras.layers.Dropout(0.3))
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

history = model.fit(train_scaled, train_target, epochs=10, verbose=0,
                    validation_data=(val_scaled, val_target))

model.save('model-whole.keras')
# h5의 경우 HDF5 포맷으로 저장
model.save_weights('model.weights.h5')

!ls -al model*
# -rw-r--r-- 1 root root 976600 Aug 17 06:32 model.weights.h5 파일 생성 확인
# -rw-r--r-- 1 root root 979411 Aug 17 06:32 model-whole.keras
model = model_fn(keras.layers.Dropout(0.3))

model.load_weights('model.weights.h5')

import numpy as np

# 해당 모델의 검증 정확도 확인(axis=-1이면 배열의 마지막 차원을 따라 최댓값 고름)
val_labels = np.argmax(model.predict(val_scaled), axis=-1)
print(np.mean(val_labels == val_target)) # 0.8809166666666667

# 동일한 모델 로드
model = keras.models.load_model('model-whole.keras')

model.evaluate(val_scaled, val_target) # [0.32992294430732727, 0.8809166550636292]

모델을 저장 후 로드 후에도 동일한 정확도를 나오는지 확인합니다.

콜백

콜백은 훈련 과정 중간에 어떤 작업을 수행할 수 있게 하는 객체입니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
model = model_fn(keras.layers.Dropout(0.3))
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

# 체크포인트 콜백: 검증 성능이 가장 좋은 모델만 저장
checkpoint_cb = keras.callbacks.ModelCheckpoint('best-model.keras', save_best_only=True)
# 20에포크를 기준으로 시작작
model.fit(train_scaled, train_target, epochs=20, verbose=0,
          validation_data=(val_scaled, val_target),
          callbacks=[checkpoint_cb])

model = keras.models.load_model('best-model.keras')
model.evaluate(val_scaled, val_target)

model = model_fn(keras.layers.Dropout(0.3))
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

# 체크포인트 콜백: 최고 성능 모델 저장
checkpoint_cb = keras.callbacks.ModelCheckpoint('best-model.keras', save_best_only=True)

# 조기 종료 콜백: 2 에포크 동안 성능 개선이 없으면 훈련 중단하고 최고 가중치 복원
early_stopping_cb = keras.callbacks.EarlyStopping(patience=2, restore_best_weights=True)

# 모델 훈련: 두 개의 콜백 함께 사용
history = model.fit(train_scaled, train_target, epochs=20, verbose=0,
                    validation_data=(val_scaled, val_target),
                    callbacks=[checkpoint_cb, early_stopping_cb])

# 실제로 훈련이 중단된 에포크 출력 (13에포크에서 중단됨)
print(early_stopping_cb.stopped_epoch)  # 13

plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['train', 'val'])
plt.show()

model.evaluate(val_scaled, val_target)

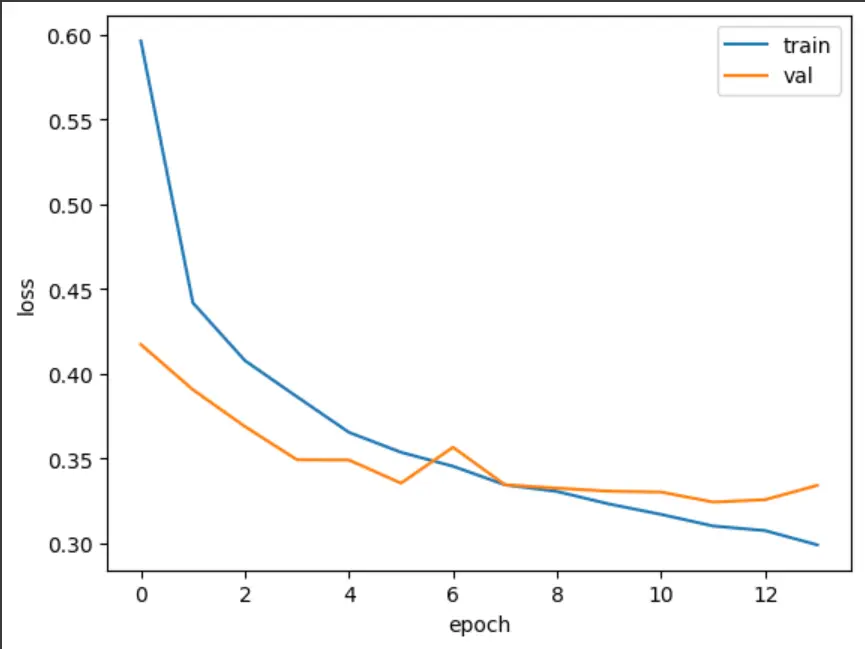
훈련 중 30%의 뉴런을 랜덤하게 비활성화해서 과적합 방지합니다.

ModelCheckpoint: 검증 성능이 개선될 때마다 모델을 자동 저장. save_best_only=True로 최고 성능 모델만 보존

EarlyStopping: patience=2로 설정해서 2 에포크 연속으로 성능이 개선되지 않으면 훈련 중단

restore_best_weights=True로 최고 성능 시점의 가중치로 복원

결과적으로로 원래 20 에포크 계획이었지만 13 에포크에서 조기 종료되어 효율적인 훈련이 이루어 진 것을 확인할 수 있습니다..!

이런 식으로 콜백을 조합하면 자동으로 최적의 모델을 찾고 불필요한 훈련 시간을 절약할 수 있습니다.

우아.. 이걸로 일단 혼공학습단 활동은 끝이 났네요. 좀 더 천천히 책 마무리해야겠습니다. 감사합니다.

기본 숙제#

내용 정리#

인공 신경망#

로지스틱 회귀로 패션 아이템 분류하기#

인공 신경망#

인공 신경망으로 패션 아이템 분류하기#

심층 신경망#

렐루 함수#

신경망 모델 훈련#

검증 손실#

드롭 아웃#

모델 저장과 복원#

콜백#

기본 숙제

내용 정리

인공 신경망

로지스틱 회귀로 패션 아이템 분류하기

인공 신경망

인공 신경망으로 패션 아이템 분류하기

심층 신경망

렐루 함수

신경망 모델 훈련

검증 손실

드롭 아웃

모델 저장과 복원

콜백